Data Structure(Types of Tree in Data Structures)

-

 

Types of Tree in Data Structures:

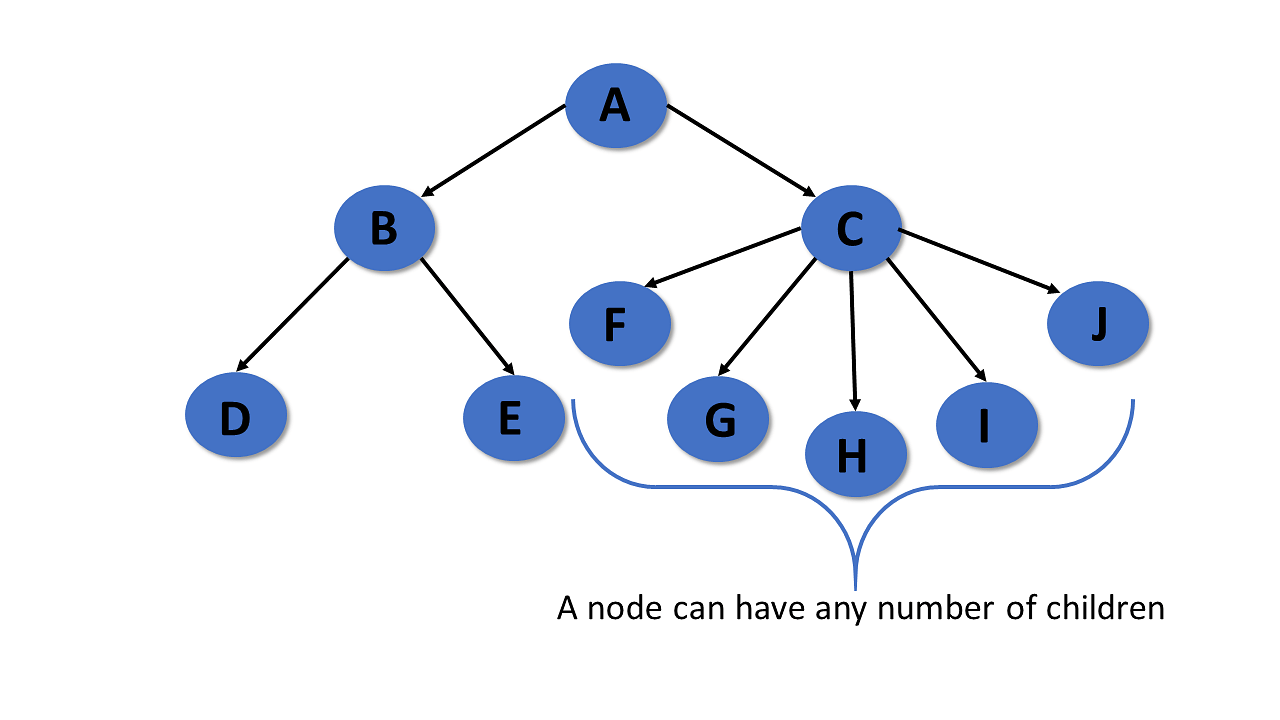
General Tree

The general tree is the type of tree where there are no constraints on the hierarchical structure.

Properties

  • The general tree follows all properties of the tree data structure.
  • A node can have any number of nodes.

Trees-Soni/general-tree

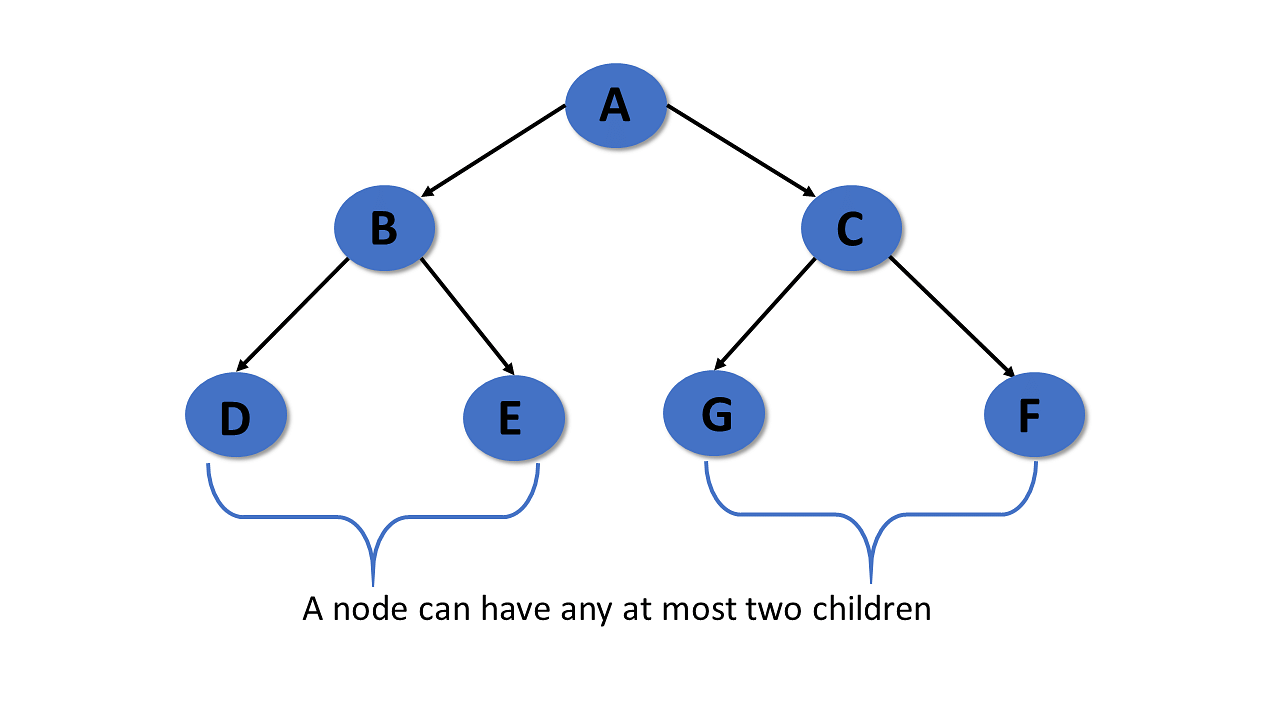
Binary Tree

A binary tree has the following properties:

Properties

  • Follows all properties of the tree data structure.
  • Binary trees can have at most two child nodes.
  • These two children are called the left child and the right child.

Trees-Soni/binary-tree.

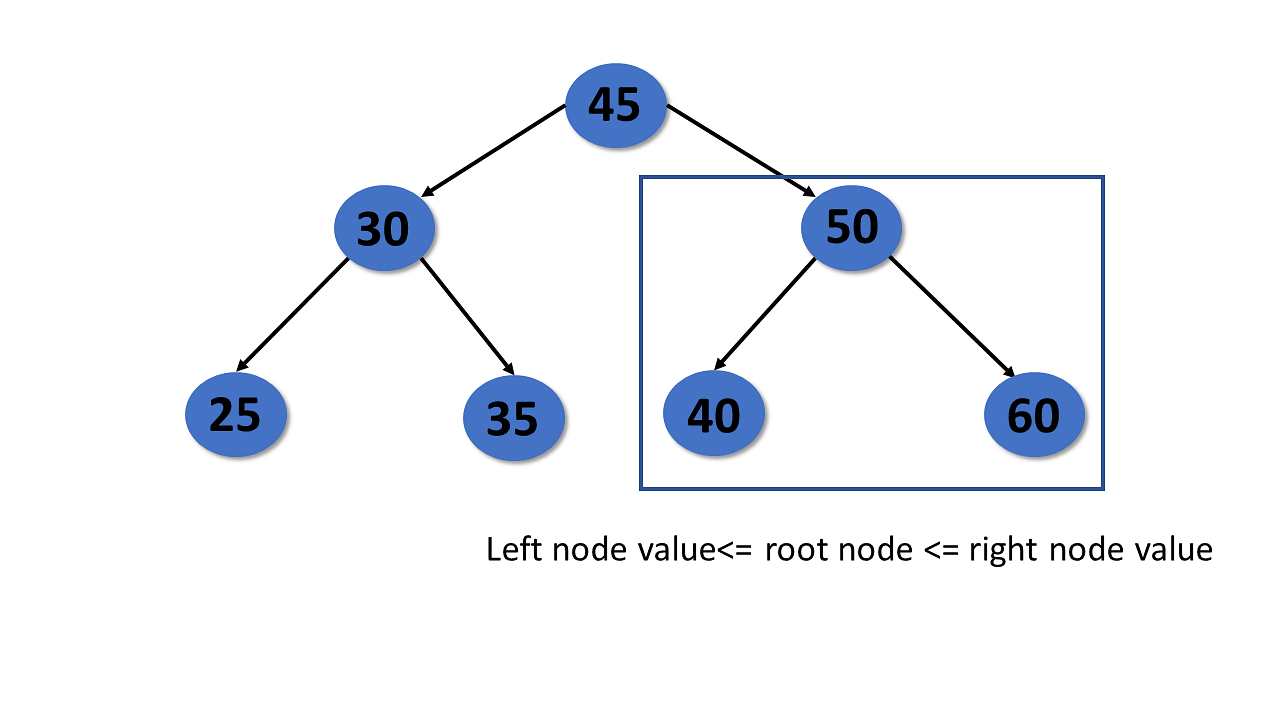
Binary Search Tree 

A binary search tree is a type of tree that is a more constricted extension of a binary tree data structure.

Properties

  • Follows all properties of the tree data structure.
  • The binary search tree has a unique property known as the binary search property. This states that the value of a left child node of the tree should be less than or equal to the parent node value of the tree. And the value of the right child node should be greater than or equal to the parent value.

Trees-Soni/binary-search-tree1.

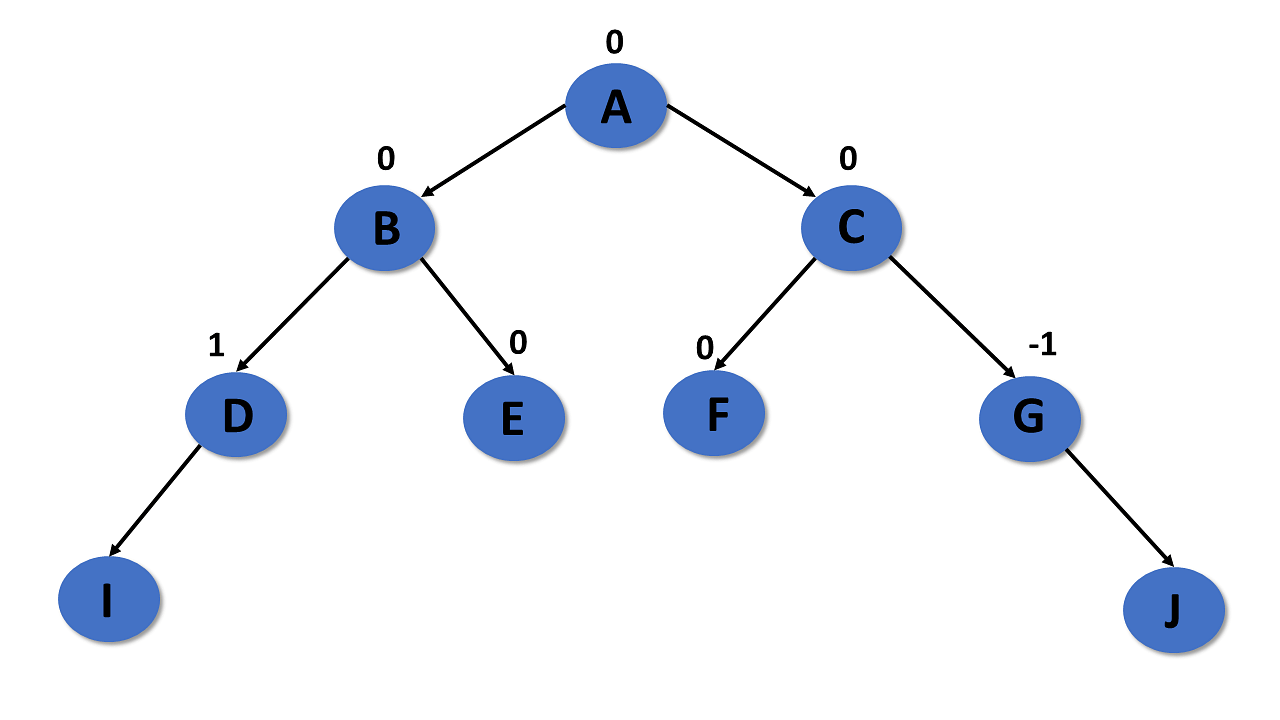
AVL Tree 

An AVL tree is a type of tree that is a self-balancing binary search tree.

Properties

  • Follows all properties of the tree data structure.
  • Self-balancing.
  • Each node stores a value called a balanced factor, which is the difference in the height of the left sub-tree and right sub-tree.
  • All the nodes in the AVL tree must have a balance factor of -1, 0, and 1.

Trees-Soni/AVL-TREE.

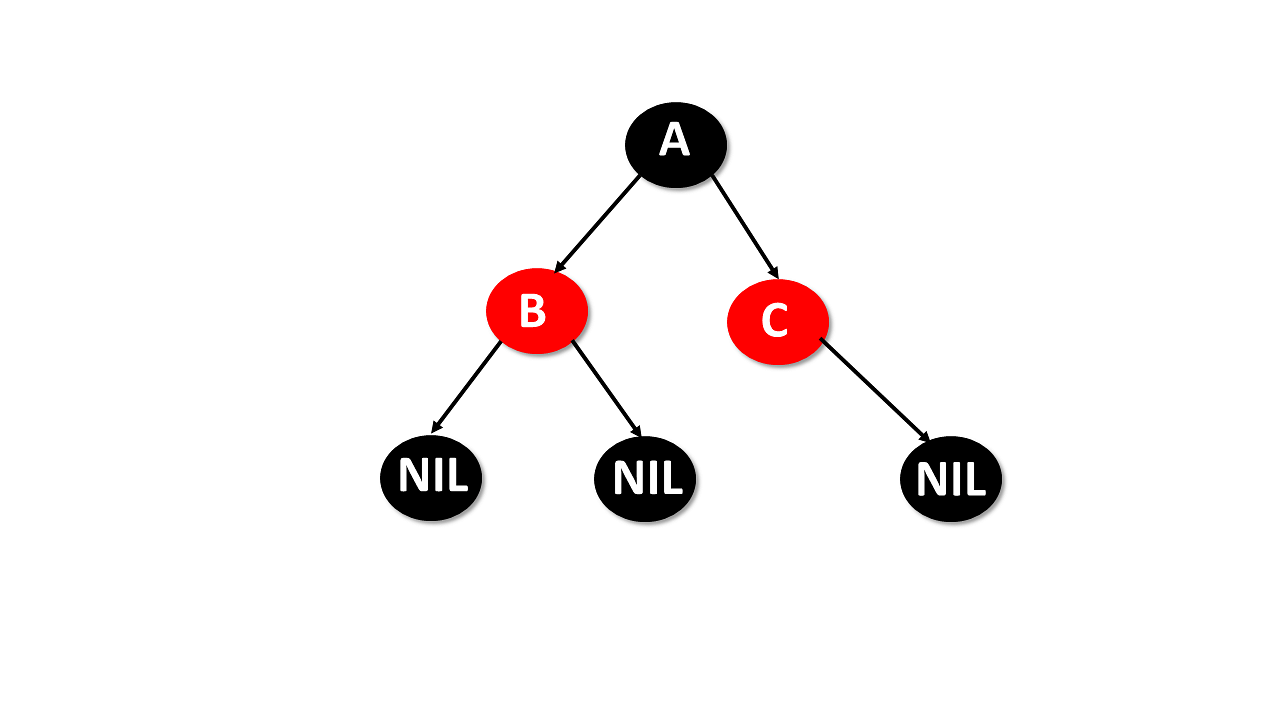
Red-Black Tree

  • A red-black tree is a self-balancing binary search tree, where each node has either the color of red or black.
  • The colors of the nodes are used to make sure that the tree remains approximately balanced during insertion and deletion.

Properties

  • Follow all properties of binary tree data structure.
  • Self-balancing.
  • Each node is either red or black.
  • The root and leaves nodes are black.
  • If the node is red, then both children are black.
  • Every path from a given node to any of its nodes must go through the same number of black nodes.

/RED-BLACK-TREE

Splay Tree

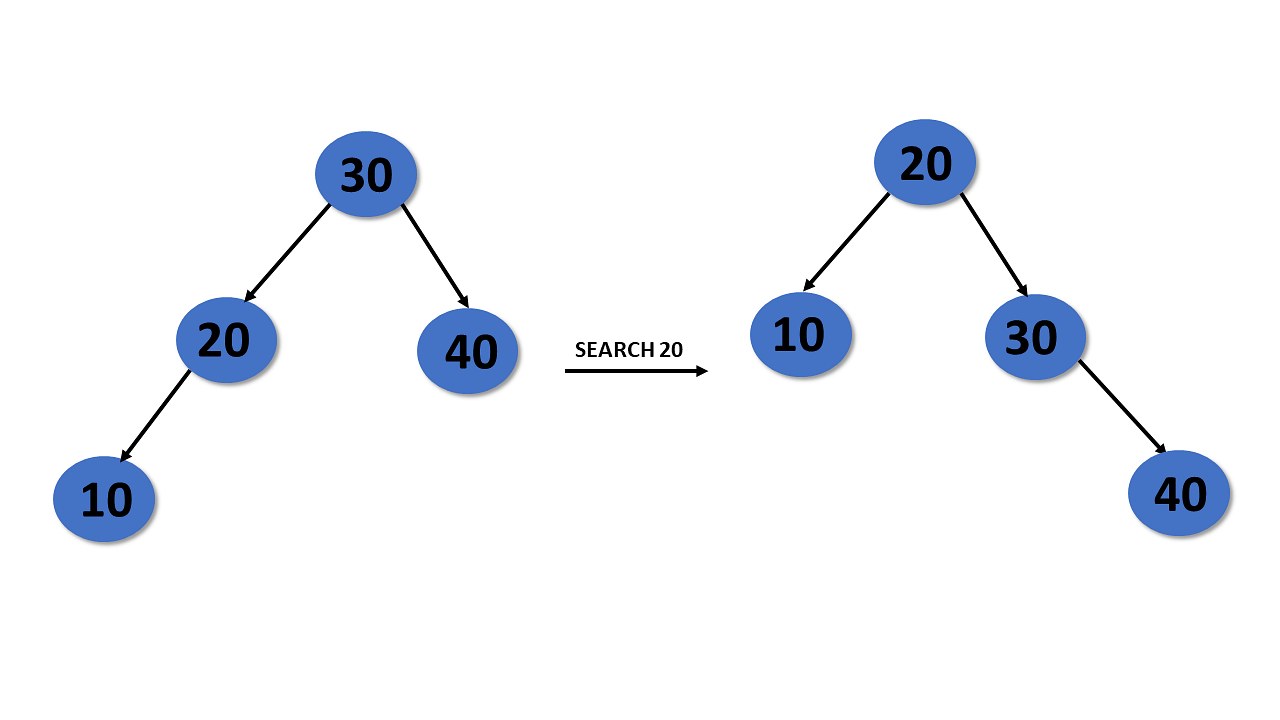
A splay tree is a self-balancing binary search tree.

Properties

  • Follows properties of binary tree data structure.
  • Self-balancing.
  • Recently accessed elements are quicker to access again.

After you perform operations such as insertion and deletion, the splay tree acts, which is called splaying. Here it rearranges the tree so that the particular elements are placed at the root of the tree.

SPLAY-TREE

Treap Tree

The Treap tree is made up of a tree, and the heap is a binary search tree.

Properties

  • Each node has two values: a key and a priority.
  • Follows a binary search tree property.
  • Priority of the treap tree follows the heap property.

TREAP-TREE.

Comments

Post a Comment

Popular posts from this blog

String Functions in C Language(C Language)

-
  C String Functions There are many important string functions defined in "string.h" library. No. Function Description 1) strlen(string_name) returns the length of string name. 2) strcpy(destination, source) copies the contents of source string to destination string. 3) strcat(first_string, second_string) concats or joins first string with second string. The result of the string is stored in first string. 4) strcmp(first_string, second_string) compares the first string with second string. If both strings are same, it returns 0. 5) strrev(string) returns reverse string. 6) strlwr(string) returns string characters in lowercase. 7) strupr(string) returns string characters in uppercase. 8) strstr( st
Read more

PHP Array Functions

-
  PHP  Array  Functions The array functions allow you to access and manipulate arrays. Simple and multi-dimensional arrays are supported. Function Description array() Creates an array array_column() Returns the values from a single column in the input array array_combine() Creates an array by using the elements from one "keys" array and one "values" array array_flip() Flips/Exchanges all keys with their associated values in an array array_pop() Deletes the last element of an array array_push() Inserts one or more elements to the end of an array array_replace() Replaces the values of the first array with the values from following arrays array_reverse() Returns an array in the reverse order array_search() Searches an array for a given value
Read more

Object Instance Working with Strings

-
  Classes are nothing without objects.We can create multiple objects from a class. Each object has all the properties and methods defined in the class, but they will have different property values. An object of a class is created using the new keyword. Example: $bsc and $bzc is instances of the class Group: <?php class Group { public $name; function set_name($name) {     $this->name=$name; } function get_name; {     return $this->name; } } $bsc=new Group(); $bzc=new Group(); $bsc->set_name('BSC'); $bzc->set_name('BZC'); echo $bsc->get_name(; echo "<br>"; echo $bzc->get_name(); ?>
Read more