Data Structures( Traversals of a graph : BFS and DFS)

-

Graph Travesals:

Graph traversal is technique used for searching a vertex in a graph. The graph traversal is also used to decide the order of vertices to be visit in the search process. A graph traversal finds the egdes to be used in the search process without creating loops that means using graph traversal we visit all verticces of graph without getting into looping path.

There are two graph traversal techniques and they are as follows...

DFS (Depth First Search)

BFS (Breadth First Search)

 DFS (Depth First Search):

DFS traversal of a graph, produces a spanning tree as final result. Spanning Tree is a graph without any loops. We use Stack data structure with maximum size of total number of vertices in the graph to implement DFS traversal of a graph.

We use the following steps to implement DFS traversal...

Step 1: Define a Stack of size total number of vertices in the graph.

Step 2: Select any vertex as starting point for traversal. Visit that vertex and push it on to the Stack.

Step 3: Visit any one of the adjacent vertex of the verex which is at top of the stack which is not visited and push it on to the stack.

Step 4: Repeat step 3 until there are no new vertex to be visit from the vertex on top of the stack.

Step 5: When there is no new vertex to be visit then use back tracking and pop one vertex from the stack.

Step 6: Repeat steps 3, 4 and 5 until stack becomes Empty.

Step 7: When stack becomes Empty, then produce final spanning tree by removing unused edges from the graph

Back tracking is coming back to the vertex from which we came to current vertex. 

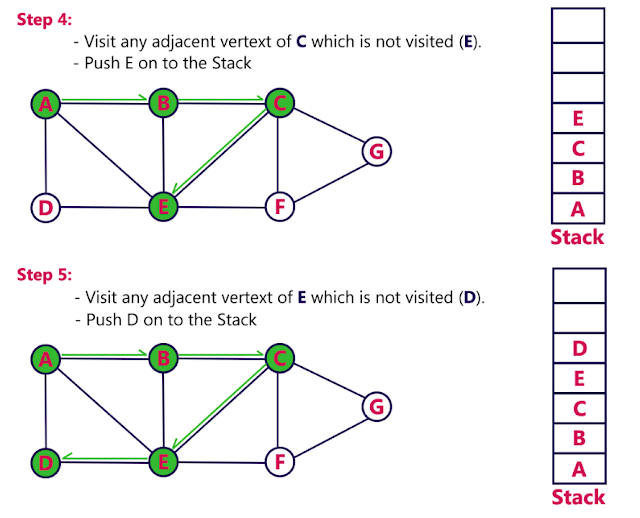
Example









BFS (Breadth First Search):

BFS traversal of a graph, produces a spanning tree as final result. Spanning Tree is a graph without any loops. We use Queue data structure with maximum size of total number of vertices in the graph to implement BFS traversal of a graph.

We use the following steps to implement BFS traversal...

Step 1: Define a Queue of size total number of vertices in the graph.

Step 2: Select any vertex as starting point for traversal. Visit that vertex and insert it into the Queue.

Step 3: Visit all the adjacent vertices of the verex which is at front of the Queue which is not visited and insert them into the Queue.

Step 4: When there is no new vertex to be visit from the vertex at front of the Queue then delete that vertex from the Queue.

Step 5: Repeat step 3 and 4 until queue becomes empty.

Step 6: When queue becomes Empty, then produce final spanning tree by removing unused edges from the graph

 Example





























Comments

Post a Comment

Popular posts from this blog

PHP Array Functions

-
  PHP  Array  Functions The array functions allow you to access and manipulate arrays. Simple and multi-dimensional arrays are supported. Function Description array() Creates an array array_column() Returns the values from a single column in the input array array_combine() Creates an array by using the elements from one "keys" array and one "values" array array_flip() Flips/Exchanges all keys with their associated values in an array array_pop() Deletes the last element of an array array_push() Inserts one or more elements to the end of an array array_replace() Replaces the values of the first array with the values from following arrays array_reverse() Returns an array in the reverse order array_search() Searches an array for a given value
Read more

String Functions in C Language(C Language)

-
  C String Functions There are many important string functions defined in "string.h" library. No. Function Description 1) strlen(string_name) returns the length of string name. 2) strcpy(destination, source) copies the contents of source string to destination string. 3) strcat(first_string, second_string) concats or joins first string with second string. The result of the string is stored in first string. 4) strcmp(first_string, second_string) compares the first string with second string. If both strings are same, it returns 0. 5) strrev(string) returns reverse string. 6) strlwr(string) returns string characters in lowercase. 7) strupr(string) returns string characters in uppercase. 8) strstr( st
Read more

Object Instance Working with Strings

-
  Classes are nothing without objects.We can create multiple objects from a class. Each object has all the properties and methods defined in the class, but they will have different property values. An object of a class is created using the new keyword. Example: $bsc and $bzc is instances of the class Group: <?php class Group { public $name; function set_name($name) {     $this->name=$name; } function get_name; {     return $this->name; } } $bsc=new Group(); $bzc=new Group(); $bsc->set_name('BSC'); $bzc->set_name('BZC'); echo $bsc->get_name(; echo "<br>"; echo $bzc->get_name(); ?>
Read more