Data Structures(Binary search in Data structures)

Binary Search

👉 Binary search is the search technique which works efficiently on the sorted lists. 

👉 Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.

👉 Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. 

👉 If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.

👉 Binary search is implemented using following steps...

• Step 1 - Read the search element from the user.
• Step 2 - Find the middle element in the sorted list.
• Step 3 - Compare the search element with the middle element in the sorted list.
• Step 4 - If both are matched, then display "Given element is found!!!" and terminate the function.
• Step 5 - If both are not matched, then check whether the search element is smaller or larger than the middle element.
• Step 6 - If the search element is smaller than middle element, repeat steps 2, 3, 4 and 5 for the left sublist of the middle element.
• Step 7 - If the search element is larger than middle element, repeat steps 2, 3, 4 and 5 for the right sublist of the middle element.
• Step 8 - Repeat the same process until we find the search element in the list or until sublist contains only one element.
• Step 9 - If that element also doesn't match with the search element, then display "Element is not found in the list!!!" and terminate the function.

BINARY_SEARCH(A, lower_bound, upper_bound, VAL)

• Step 1: [INITIALIZE] SET BEG = lower_bound
  END = upper_bound, POS = - 1
• Step 2: Repeat Steps 3 and 4 while BEG <=END
• Step 3: SET MID = (BEG + END)/2
• Step 4: IF A[MID] = VAL
  SET POS = MID
  PRINT POS
  Go to Step 6
  ELSE IF A[MID] > VAL
  SET END = MID - 1
  ELSE
  SET BEG = MID + 1
  [END OF IF]
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
  [END OF IF]
• Step 6: EXIT

  Complexity

SN	Performance	Complexity
1	Worst case	O(log n)
2	Best case	O(1)
3	Average Case	O(log n)
4	Worst case space complexity	O(1)

Example

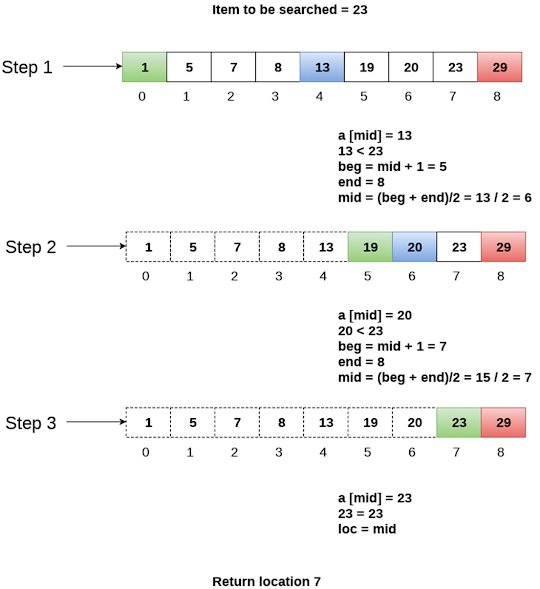
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.

In 1^st step :

1.    BEG = 0   

2.    END = 8ron  

3.    MID = 4   

4.    a[mid] = a[4] = 13 < 23, therefore  

in Second step:

1.    Beg = mid +1 = 5   

2.    End = 8  

3.    mid = 13/2 = 6    

4.    a[mid] = a[6] = 20 < 23, therefore;   

in third step:

1.    beg = mid + 1 = 7   

2.    End = 8   

3.    mid = 15/2 = 7  

4.    a[mid] = a[7]   

5.    a[7] = 23 = item;   

6.    therefore, set location = mid;   

7.    The location of the item will be 7.   

 

Implementation of Binary Search Algorithm :

#include<stdio.h>
#include<conio.h>

void main()
{
   int first, last, middle, size, i, sElement, list[100];
   clrscr();
 
   printf("Enter the size of the list: ");
   scanf("%d",&size);
 
   printf("Enter %d integer values in Assending order\n", size);
 
   for (i = 0; i < size; i++)
      scanf("%d",&list[i]);
 
   printf("Enter value to be search: ");
   scanf("%d", &sElement);
 
   first = 0;
   last = size - 1;
   middle = (first+last)/2;
 
   while (first <= last) {
      if (list[middle] < sElement)
         first = middle + 1;    
      else if (list[middle] == sElement) {
         printf("Element found at index %d.\n",middle);
         break;
      }
      else
         last = middle - 1;
 
      middle = (first + last)/2;
   }
   if (first > last)
      printf("Element Not found in the list.");
   getch();  
}

Output